De Bruijn Graph Assembly

name: inverse
layout: true
class: center, middle, inverse

</span></div>

</span></div>

---

# De Bruijn Graph Assembly

<div class="contributors-line">
		Authors: 
<a href="/training-material/hall-of-fame/slugger70/" class="contributor-badge contributor-slugger70"><img src="https://avatars.githubusercontent.com/slugger70?s=27" alt="Avatar">Simon Gladman</a>

</div>

<div class="footnote" style="bottom: 8em;"><i class="far fa-calendar" aria-hidden="true"></i><span class="visually-hidden">last_modification</span> Updated: Feb 7, 2022</div>

<div class="footnote" style="bottom: 6em;">

<i class="fas fa-file-alt" aria-hidden="true"></i><span class="visually-hidden">text-document</span><a href="slides-plain.html"> Plain-text slides</a>
</div>

<div class="footnote" style="bottom: 2em;">
    <strong>Tip: </strong>press <kbd>P</kbd> to view the presenter notes
    | <i class="fa fa-arrows" aria-hidden="true"></i><span class="visually-hidden">arrow-keys</span> Use arrow keys to move between slides

</div>

???
Presenter notes contain extra information which might be useful if you intend to use these slides for teaching.

Press `P` again to switch presenter notes off

Press `C` to create a new window where the same presentation will be displayed.
This window is linked to the main window. Changing slides on one will cause the
slide to change on the other.

Useful when presenting.

---

## Requirements

Before diving into this slide deck, we recommend you to have a look at:

- [Introduction to Galaxy Analyses](/training-material/topics/introduction)

- [Sequence analysis](/training-material/topics/sequence-analysis)
    - Quality Control: [<i class="fab fa-slideshare" aria-hidden="true"></i><span class="visually-hidden">slides</span> slides](/training-material/topics/sequence-analysis/tutorials/quality-control/slides.html) - [<i class="fas fa-laptop" aria-hidden="true"></i><span class="visually-hidden">tutorial</span> hands-on](/training-material/topics/sequence-analysis/tutorials/quality-control/tutorial.html)

---

### <i class="far fa-question-circle" aria-hidden="true"></i><span class="visually-hidden">question</span> Questions

- What are the factors that affect genome assembly?

- How does Genome assembly work?

---

### <i class="fas fa-bullseye" aria-hidden="true"></i><span class="visually-hidden">objectives</span> Objectives

- Perform an optimised Velvet assembly with the Velvet Optimiser

- Compare this assembly with those we did in the basic tutorial

- Perform an assembly using the SPAdes assembler.

---

.enlarge120[

# ***De novo* Genome Assembly**

## **Part 2: De Bruijn Graph Assembly**

]

#### With thanks to T Seemann, D Bulach, I Cooke and Simon Gladman
---
.enlarge120[
# **de Bruijn Graphs**
]
.pull-left[
* Named after Nicolaas Govert de Bruijn
* Directed graph representing overlaps between sequences of symbols
* Sequences can be reconstructed by moving between nodes in graph
]
.pull-right[
.image-50[![black and white image of a man wearing glasses](../../images/debruijn.png)]
]
---
.enlarge120[# **de Bruijn Graphs**

* A directed graph of sequences of symbols
* Nodes in the graph are k-mers
* Edges represent consecutive k-mers (which overlap by k-1 symbols)
]
Consider the 2 symbol alphabet (0 & 1) de Bruijn Graph for k =3
![every permutation of 3 0s and/or 1s is shown, each is a node. Lines connect ones that share at least 2 overlap.](../../images/debruijn01.png)
---
.enlarge120[# **Producing sequences**

* Sequences of symbols are produced by moving through the graph
]
![Same graph as before with arrows listing a path through the graph. Nodes 111, 110, 100, and 000 combine into 111000.](../../images/debruijn02.png)

---
.enlarge120[
# **K-mers?**       .pull-right[.image-25[![Special K Logo](../../images/specialk.png)]]

<hr>
* To be able to use de Bruijn graphs, we need reads of length **L** to overlap by **L-1** bases.
* Not all reads will overlap another read perfectly.
  * Read errors
  * Coverage "holes"
* Not all reads are the same length (depending on technology and quality cleanup)

***To help us get around these problems, we use all k-length subsequences of the reads, these are the k-mers.***
]
---
.enlarge120[
# **What are K-mers?**       .pull-right[.image-25[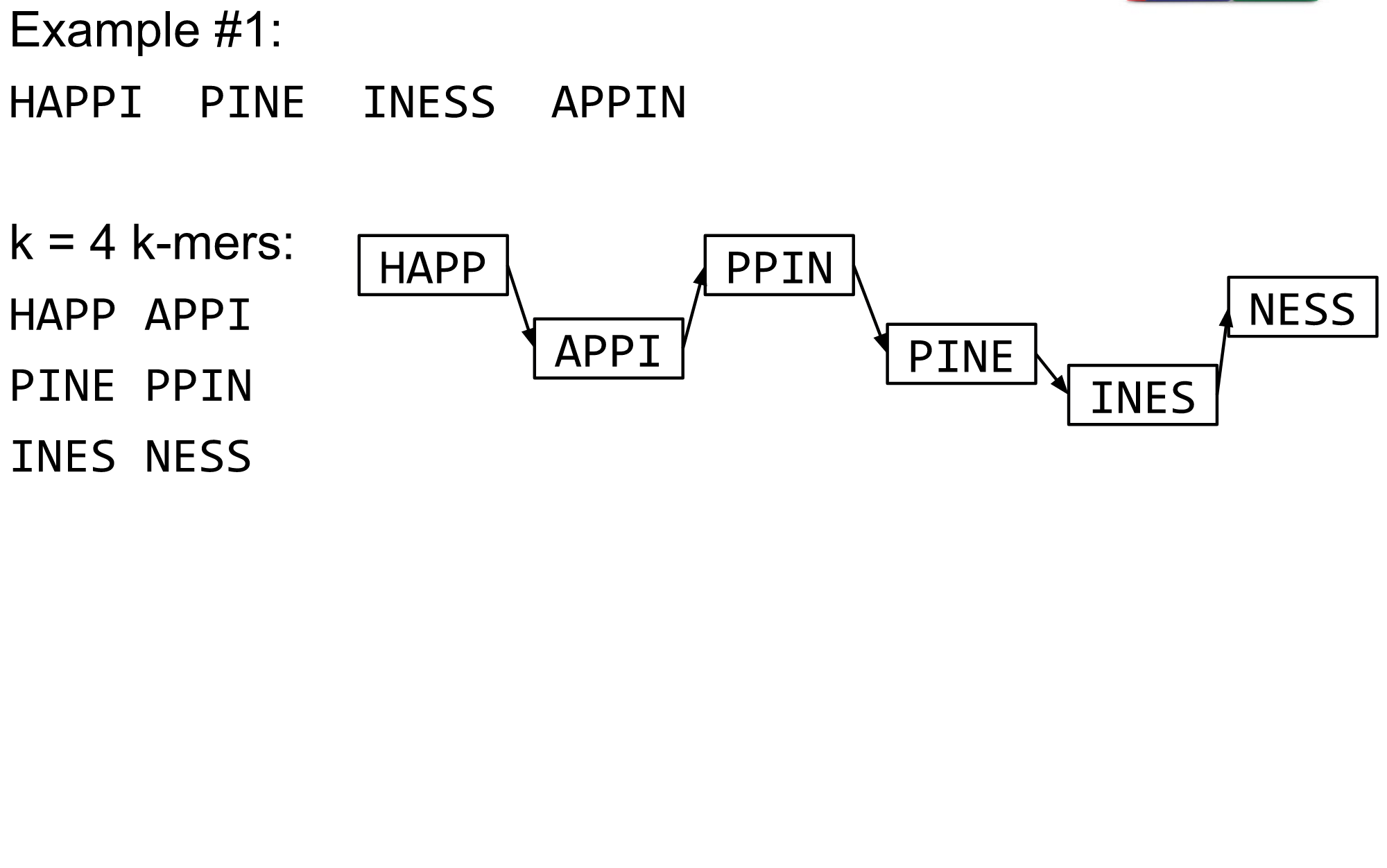![Special K Logo](../../images/specialk.png)]]]
![k=12 kmers show three sequences with length 12 overlapping. For k=5 10 different shorter sequences are shown.](../../images/kmers01.png)

---
.enlarge120[
# **K-mers de Bruijn graph**       .pull-right[.image-25[![Wooden blocks with letters A, B, C.](../../images/abc.png)]]]
![An example of happiness is given with 4 fragments, happi, pine, iness, appin.](../../images/ex1-1.png)
---
.enlarge120[
# **K-mers de Bruijn graph**       .pull-right[.image-25[![Wooden blocks with letters A, B, C.](../../images/abc.png)]]]
![all 4-mers are shown from those 5-mers, so happi becomes happ and appi. These are then uniqued.](../../images/ex1-2.png)
---
.enlarge120[
# **K-mers de Bruijn graph**       .pull-right[.image-25[![Wooden blocks with letters A, B, C.](../../images/abc.png)]]]
![A graph is drawn based on overlaps between those 4-mers.](../../images/ex1-3.png)
---
.enlarge120[
# **K-mers de Bruijn graph**       .pull-right[.image-25[![Wooden blocks with letters A, B, C.](../../images/abc.png)]]]
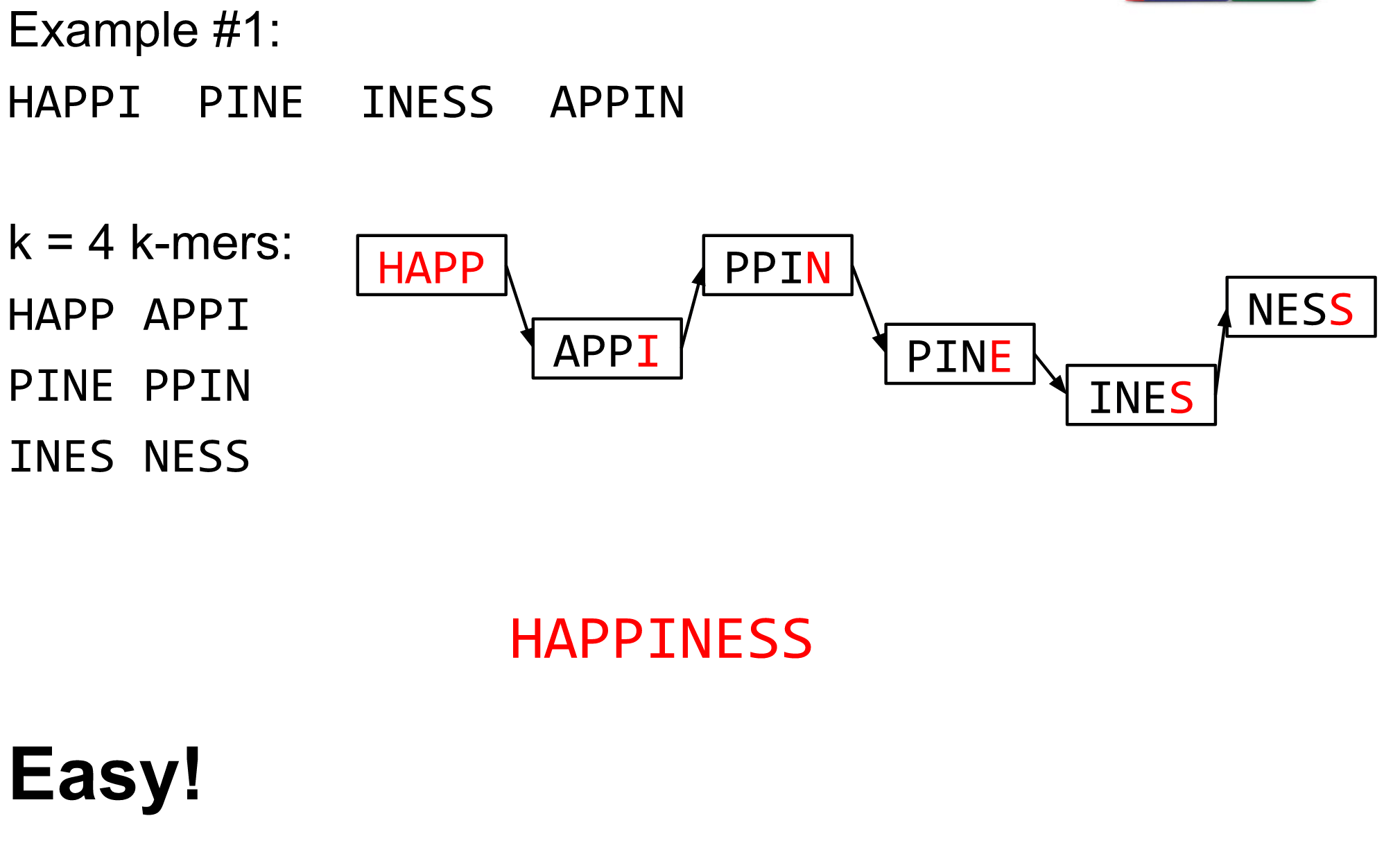![The graph is collapsed into the word happiness, success.](../../images/ex1-4.png)

---
.enlarge120[
# **The problem of repeats**       .pull-right[.image-25[![Repeat icon](../../images/repeatlogo.png)]]]
![A second example with the word mississippi is shown. The fragments are now missis, ssissi, ssippi.](../../images/ex2-1.png)
---
.enlarge120[
# **The problem of repeats**       .pull-right[.image-25[![Repeat icon](../../images/repeatlogo.png)]]]
![All 4-mers are generated so missis becomes miss, issi, and ssis. These are then uniqued to get 7 unique 4-mers.](../../images/ex2-2.png)
---
.enlarge120[
# **The problem of repeats**       .pull-right[.image-25[![Repeat icon](../../images/repeatlogo.png)]]]
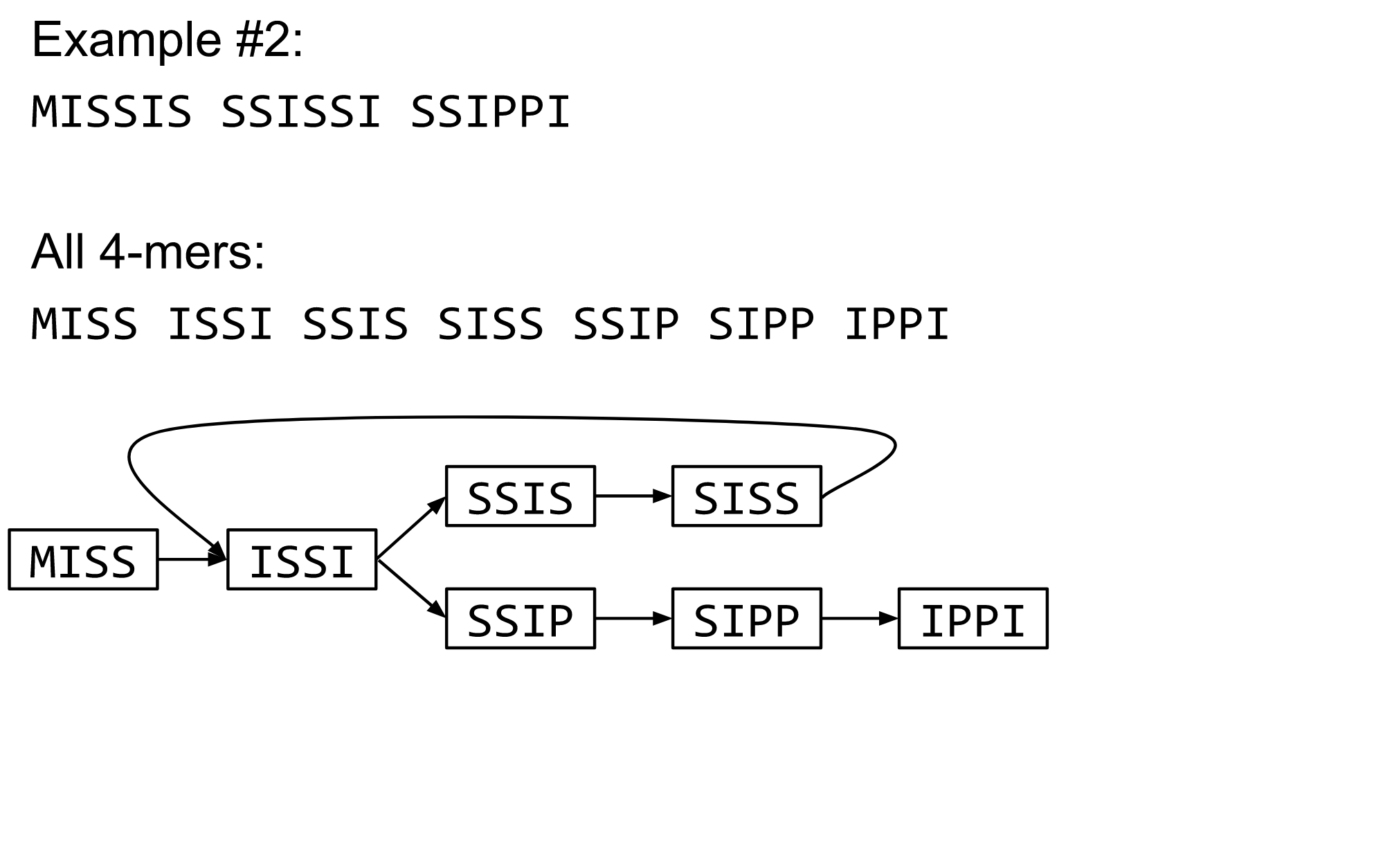![A graph is generated but this graph is more complex and has a loop.](../../images/ex2-3.png)
---
.enlarge120[
# **The problem of repeats**       .pull-right[.image-25[![Repeat icon](../../images/repeatlogo.png)]]]
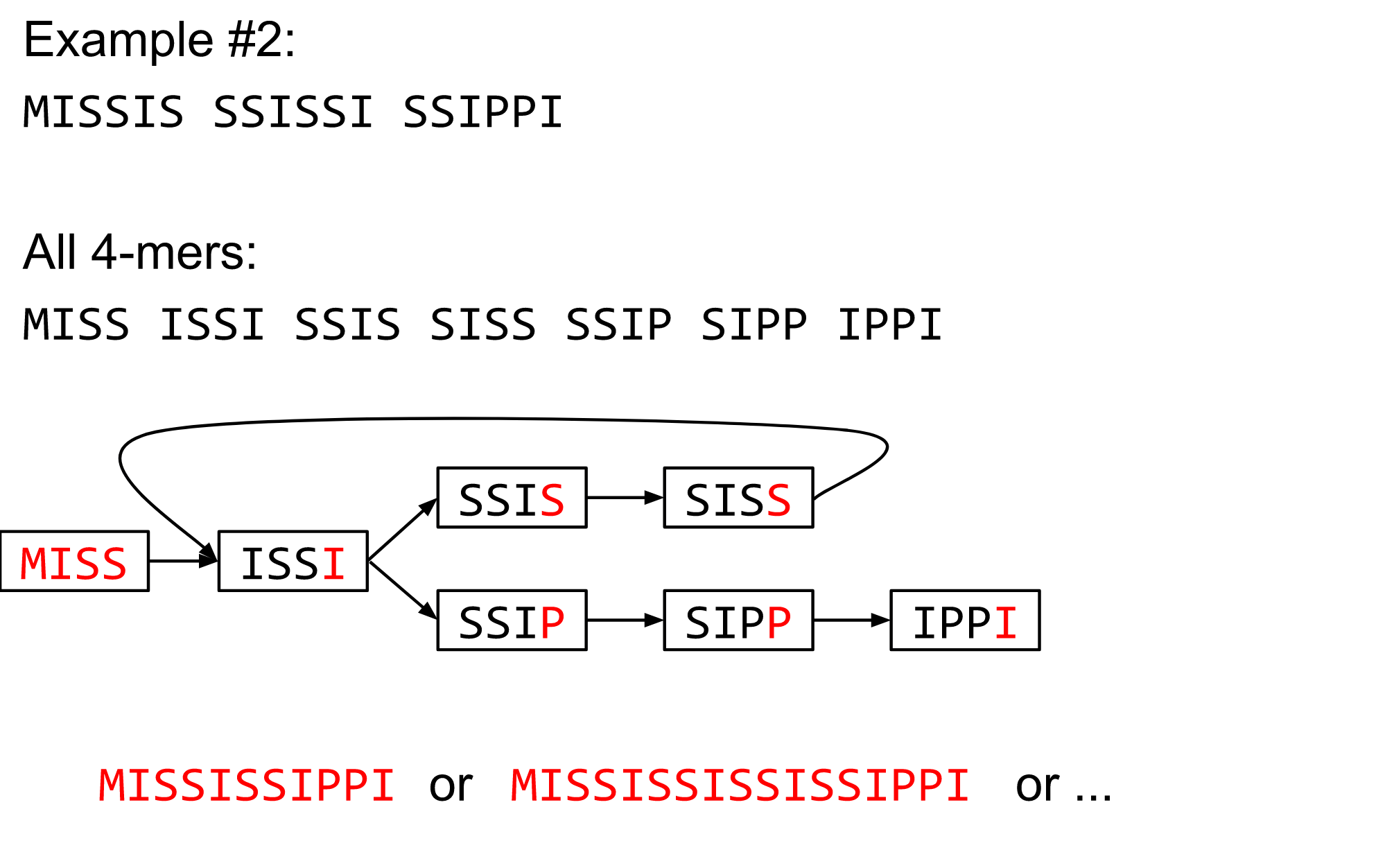![This graph is walked and now the results are shown, mississippi, mississississippi, or more could be found by following the loop repeatedly.](../../images/ex2-4.png)
---
.enlarge120[
# **Different k**       .pull-right[.image-25[![Letter K](../../images/bigk.png)]]]
![The same mississippi example from the start.](../../images/ex2a-1.png)
---
.enlarge120[
# **Different k**       .pull-right[.image-25[![Letter K](../../images/bigk.png)]]]
![Instead of 4-mers, we now produce 5-mers.](../../images/ex2a-2.png)
---
.enlarge120[
# **Different k**       .pull-right[.image-25[![Letter K](../../images/bigk.png)]]]
![The graph is produced, and now there are two disconnected sets of nodes.](../../images/ex2a-3.png)
---
.enlarge120[
# **Different k**       .pull-right[.image-25[![Letter K](../../images/bigk.png)]]]
![When collapsing this graph we see two results, MISSISSIS and SSIPPI.](../../images/ex2a-4.png)

---
.enlarge120[
# **Choose k wisely**       .pull-right[.image-25[![An old man from some movie.](../../images/wisely.png)]]]

.enlarge120[
* Lower k
  * More connections
  * Less chance of resolving small repeats
  * Higher k-mer coverage

* Higher k
  * Less connections
  * More chance of resolving small repeats
  * Lower k-mer coverage

***Optimum value for k will balance these effects.***

]
---
.enlarge120[
# **Read errors**       .pull-right[.image-25[![hazard symbol](../../images/hazardsymbol.png)]]]
.image-75[![Example 3, happiness again, with fragments happi, iness, aplin, pinet](../../images/ex3-head.png)]
![Blank image](../../images/blank.png)
---
.enlarge120[
# **Read errors**       .pull-right[.image-25[![hazard symbol](../../images/hazardsymbol.png)]]]
.image-75[![Happiness example 5-mers](../../images/ex3-head.png)]
![all 3-mers are produced](../../images/ex3-2.png)
---
.enlarge120[
# **Read errors**       .pull-right[.image-25[![hazard symbol](../../images/hazardsymbol.png)]]]
.image-75[![Happiness example 5-mers](../../images/ex3-head.png)]
![The three mers are collapsed into an overlap graph](../../images/ex3-3.png)
---
.enlarge120[
# **Read errors**       .pull-right[.image-25[![hazard symbol](../../images/hazardsymbol.png)]]]
.image-75[![Happiness example 5-mers](../../images/ex3-head.png)]
![The graph is coloured and six contigs are produced based on overlaps.](../../images/ex3-4.png)

---
.enlarge120[
# **More coverage**       .pull-right[.image-50[![hazard symbol](../../images/depthlogo.png)]]]

.enlarge120[
* Errors won't be duplicated in every read
* Most reads will be error free
* We can count the frequency of each k-mer
* Annotate the graph with the frequencies
* Use the frequency data to clean the de Bruijn graph

***More coverage depth will help overcome errors!***
]
---
.enlarge120[
# **Read errors revisited**       .pull-right[.image-50[![hazard symbol](../../images/hazardsymbol.png)]]]
![Same happiness example, all three mers are present, but now the counts are shown. One path has many more counts than the other. Text asks which path looks most valid? why?](../../images/ex3a.png)

---
.enlarge120[
# **Another parameter - coverage cutoff**]

.enlarge120[
* At what point is a low coverage indicative of an error?
* Can we ignore low coverage nodes and paths?
* This is a new assembly parameter

***Coverage cutoff***
]

---
.enlarge120[
# **de Bruijn graph assembly process**]

.enlarge120[
1. Select a value for k
2. "Hash" the reads (make the kmers)
3. Count the kmers
4. Make the de Bruijn graph
5. **Perform graph simplification steps** - use cov cutoff
6. Read off contigs from simplified graph

]

---
.enlarge120[
# **Graph simplification**]

## Step 1: Chain merging

![Looking at a doubly connected graph with forward/reverse sequences and piles of overlaps. Nodes are connected with lines. One node is labelled as already merged, and two nodes sharing a prefix are labelled as further merging possible.](../../images/tipclipping.png)

---
.enlarge120[
# **Graph simplification**]

## Step 2: Tip clipping

![a graph with every node doubled for forward/reverse strands is shown, clip tips if the length of the tip of the node is less than 2 times k.](../../images/shortnodes.png)

---
.enlarge120[
# **Graph simplification**]

.pull-left[
![Three graphs are shown, B, C, and D. B is the most complex, C combines two nodes B and B prime, while D collapses even more nodes to further simplify the graph.](../../images/bubblemerging.png)
]
.pull-right[
## Step 3: Bubble collapsing

* Detect redundant paths through graph
* Compare the paths using sequence alignment
* If similar, merge the paths

.reduce70[Image: Zerbino & Birney 2008]
]

---
.enlarge120[
# **Graph simplification**

## Step 4: Remove low coverage nodes

* Remove erroneous nodes and connections using the "coverage cutoff"
* Genuine short nodes will have a high coverage

]
---
.enlarge120[
# **Make contigs**

* Find an unbalanced node in the graph
* Follow the chain of nodes and "read off" the bases to produce the contigs
* Where there is an ambiguous divergence/convergence, stop the current contig and start a new one.
* Re-trace the reads through the contigs to help with repeat resolution

]

---
.enlarge120[
# **Velvet**

Velvet has two separate programs:

* Velveth
  * Makes the k-mers and
  * Efficiently counts (hashes) them
  * All in O(N) time

* Velvetg
  * Makes the graph - O(U) time. U = unique k-mers.
  * Simplifies it
  * Makes contigs - O(E) time. E = edges in graph

But: You need to choose **k** and **c** wisely!

]

---
.enlarge120[
# **Velvet - Paired end scaffolding**

* Breadcrumb algorithm
]

![Two boxes A and B are at opposite ends, there are many nodes along a line between them, and some sitting outside of the graph or otherwise weirdly connected.](../../images/breadcrumb.png)

---
.enlarge120[
# **Extensions of the idea**
]
---
.enlarge120[
# **SPAdes**     .pull-right[.image-50[![spades logo](../../images/spades.png)]]]

.enlarge120[
* de Bruijn graph assembler by Pavel Pevzner's group out of St. Petersburg

* Uses multiple k-mers to build the graph
  * Graph has connectivity **and** specificity
  * Usually use a low, medium and high k-mer size together.

* Performs error correction on the reads first

* Maps reads back to the contigs and scaffolds as a check

* Under active development

* Much slower than Velvet
* Should be used in preference to Velvet now.

]
---
.enlarge120[
# **A move back to OLC**]

.pull-left[
.enlarge120[
* New long read technologies
  * PacBio and MinIon

* Assemblers: HGap, CANU
  * Use overlap, layout consensus approach

* CANU can perform hybrid assemblies with long and short reads
]
]

.pull-right[
![image of a minion connected to a computer via a cable. Below a man stands next to a very large machine.](../../images/minionpacbio.png)
]
---
.enlarge120[# **Bandage**

* Assembly graph viewer and manipulator
* Written by Ryan Wick of Centre for Systems Genomics - Uni. Melbourne, Australia
]
![A screenshot of the bandage gui showning drawing options on left and a middle window with a close up of a genome assembly graph.](../../images/bandage.png)

---
### <i class="fas fa-key" aria-hidden="true"></i><span class="visually-hidden">keypoints</span> Key points

- We learned about how the choice of k-mer size will affect assembly outcomes

- We learned about the strategies that assemblers use to make reference genomes

- We performed a number of assemblies with Velvet and SPAdes.

- You should use SPAdes or another more modern assembler than Velvet for actual assemblies now.

---

## Thank You!

This material is the result of a collaborative work. Thanks to the [Galaxy Training Network](https://training.galaxyproject.org) and all the contributors!

</div>

</div>

<a rel="license" href="https://creativecommons.org/licenses/by/4.0/">
This material is licensed under the Creative Commons Attribution 4.0 International License</a>.